I. ບົດນໍາ
ນ້ຳສາມາດຈູດທຽນໄດ້, ມັນເປັນຄວາມຈິງບໍ? ມັນເປັນຄວາມຈິງ!
ມັນເປັນຄວາມຈິງບໍ່ວ່າງູຢ້ານ realgar? ມັນເປັນຄວາມຈິງ!
ສິ່ງທີ່ພວກເຮົາຈະສົນທະນາໃນມື້ນີ້ແມ່ນ:
ການແຊກແຊງສາມາດປັບປຸງຄວາມຖືກຕ້ອງຂອງການວັດແທກໄດ້, ມັນເປັນຄວາມຈິງບໍ?
ພາຍໃຕ້ສະຖານະການປົກກະຕິ, ການແຊກແຊງແມ່ນສັດຕູທຳມະຊາດຂອງການວັດແທກ. ການແຊກແຊງຈະຫຼຸດຜ່ອນຄວາມຖືກຕ້ອງຂອງການວັດແທກ. ໃນກໍລະນີທີ່ຮ້າຍແຮງ, ການວັດແທກຈະບໍ່ໄດ້ຮັບການປະຕິບັດຕາມປົກກະຕິ. ຈາກທັດສະນະນີ້, ການແຊກແຊງສາມາດປັບປຸງຄວາມຖືກຕ້ອງຂອງການວັດແທກ, ເຊິ່ງບໍ່ຖືກຕ້ອງ!
ເຖິງຢ່າງໃດກໍ່ຕາມ, ນີ້ແມ່ນກໍລະນີສະເໝີໄປບໍ? ມີສະຖານະການທີ່ການແຊກແຊງບໍ່ໄດ້ຫຼຸດຜ່ອນຄວາມຖືກຕ້ອງຂອງການວັດແທກ, ແຕ່ແທນທີ່ຈະປັບປຸງມັນບໍ?
ຄຳຕອບແມ່ນແມ່ນແລ້ວ!
2. ຂໍ້ຕົກລົງການແຊກແຊງ
ສົມທົບກັບສະຖານະການຕົວຈິງ, ພວກເຮົາໄດ້ຕົກລົງເຫັນດີກ່ຽວກັບການແຊກແຊງດັ່ງຕໍ່ໄປນີ້:
- ການແຊກແຊງບໍ່ມີອົງປະກອບ DC. ໃນການວັດແທກຕົວຈິງ, ການແຊກແຊງສ່ວນໃຫຍ່ແມ່ນການແຊກແຊງ AC, ແລະສົມມຸດຕິຖານນີ້ແມ່ນສົມເຫດສົມຜົນ.
- ເມື່ອປຽບທຽບກັບແຮງດັນໄຟຟ້າກະແສตรงທີ່ວັດແທກໄດ້, ຄວາມກວ້າງຂອງການແຊກແຊງແມ່ນຂ້ອນຂ້າງນ້ອຍ. ອັນນີ້ສອດຄ່ອງກັບສະຖານະການຕົວຈິງ.
- ການແຊກແຊງແມ່ນສັນຍານທີ່ເປັນໄລຍະ, ຫຼືຄ່າສະເລ່ຍແມ່ນສູນພາຍໃນໄລຍະເວລາທີ່ກຳນົດໄວ້. ຈຸດນີ້ບໍ່ຈຳເປັນຕ້ອງເປັນຄວາມຈິງໃນການວັດແທກຕົວຈິງ. ຢ່າງໃດກໍຕາມ, ເນື່ອງຈາກການແຊກແຊງໂດຍທົ່ວໄປແມ່ນສັນຍານ AC ຄວາມຖີ່ສູງ, ສຳລັບການແຊກແຊງສ່ວນໃຫຍ່, ສົນທິສັນຍາຂອງຄ່າສະເລ່ຍສູນແມ່ນສົມເຫດສົມຜົນສຳລັບໄລຍະເວລາທີ່ຍາວກວ່າ.
3. ຄວາມຖືກຕ້ອງຂອງການວັດແທກພາຍໃຕ້ການແຊກແຊງ
ເຄື່ອງມືວັດແທກໄຟຟ້າ ແລະ ມິເຕີສ່ວນໃຫຍ່ໃນປັດຈຸບັນໃຊ້ຕົວແປງ AD, ແລະ ຄວາມຖືກຕ້ອງຂອງການວັດແທກຂອງມັນແມ່ນກ່ຽວຂ້ອງຢ່າງໃກ້ຊິດກັບຄວາມລະອຽດຂອງຕົວແປງ AD. ໂດຍທົ່ວໄປ, ຕົວແປງ AD ທີ່ມີຄວາມລະອຽດສູງກວ່າຈະມີຄວາມຖືກຕ້ອງຂອງການວັດແທກສູງກວ່າ.
ເຖິງຢ່າງໃດກໍ່ຕາມ, ຄວາມລະອຽດຂອງ AD ແມ່ນມີຈຳກັດສະເໝີ. ສົມມຸດວ່າຄວາມລະອຽດຂອງ AD ແມ່ນ 3 ບິດ ແລະ ແຮງດັນວັດແທກສູງສຸດແມ່ນ 8V, ຕົວແປງ AD ແມ່ນເທົ່າກັບຂະໜາດທີ່ແບ່ງອອກເປັນ 8 ສ່ວນ, ແຕ່ລະສ່ວນແມ່ນ 1V. ແມ່ນ 1V. ຜົນການວັດແທກຂອງ AD ນີ້ແມ່ນຈຳນວນເຕັມສະເໝີ, ແລະ ສ່ວນທົດສະນິຍົມແມ່ນຖືກນຳໄປ ຫຼື ຖືກຖິ້ມສະເໝີ, ເຊິ່ງສົມມຸດວ່າຖືກນຳໄປໃນເອກະສານນີ້. ການນຳໄປ ຫຼື ການຖິ້ມຈະເຮັດໃຫ້ເກີດຄວາມຜິດພາດໃນການວັດແທກ. ຕົວຢ່າງ, 6.3V ແມ່ນຫຼາຍກວ່າ 6V ແລະ ໜ້ອຍກວ່າ 7V. ຜົນການວັດແທກ AD ແມ່ນ 7V, ແລະມີຄວາມຜິດພາດ 0.7V. ພວກເຮົາເອີ້ນຄວາມຜິດພາດນີ້ວ່າ ຄວາມຜິດພາດໃນການວັດແທກ AD.
ເພື່ອຄວາມສະດວກໃນການວິເຄາະ, ພວກເຮົາສົມມຸດວ່າເຄື່ອງຊັ່ງ (ຕົວແປງ AD) ບໍ່ມີຄວາມຜິດພາດໃນການວັດແທກອື່ນໆ ຍົກເວັ້ນຄວາມຜິດພາດໃນການວັດແທກປະລິມານ AD.
ບັດນີ້, ພວກເຮົາໃຊ້ສອງຂະໜາດທີ່ຄືກັນເພື່ອວັດແທກແຮງດັນໄຟຟ້າ DC ສອງອັນທີ່ສະແດງຢູ່ໃນຮູບທີ 1 ໂດຍບໍ່ມີການແຊກແຊງ (ສະຖານະການທີ່ດີທີ່ສຸດ) ແລະ ດ້ວຍການແຊກແຊງ.
ດັ່ງທີ່ສະແດງຢູ່ໃນຮູບທີ 1, ແຮງດັນໄຟຟ້າ DC ທີ່ວັດແທກໄດ້ຕົວຈິງແມ່ນ 6.3V, ແລະແຮງດັນໄຟຟ້າ DC ໃນຮູບເບື້ອງຊ້າຍບໍ່ມີການແຊກແຊງໃດໆ, ແລະມັນເປັນຄ່າຄົງທີ່ໃນຄ່າ. ຮູບເບື້ອງຂວາສະແດງໃຫ້ເຫັນກະແສໄຟຟ້າໂດຍກົງທີ່ຖືກລົບກວນໂດຍກະແສໄຟຟ້າສະລັບ, ແລະມີຄວາມຜັນຜວນທີ່ແນ່ນອນໃນຄ່າ. ແຮງດັນໄຟຟ້າ DC ໃນແຜນວາດເບື້ອງຂວາແມ່ນເທົ່າກັບແຮງດັນໄຟຟ້າ DC ໃນແຜນວາດເບື້ອງຊ້າຍຫຼັງຈາກກຳຈັດສັນຍານແຊກແຊງ. ສີ່ຫຼ່ຽມມົນສີແດງໃນຮູບສະແດງເຖິງຜົນການປ່ຽນແປງຂອງຕົວແປງ AD.

ແຮງດັນໄຟຟ້າ DC ທີ່ເໝາະສົມໂດຍບໍ່ມີການແຊກແຊງ
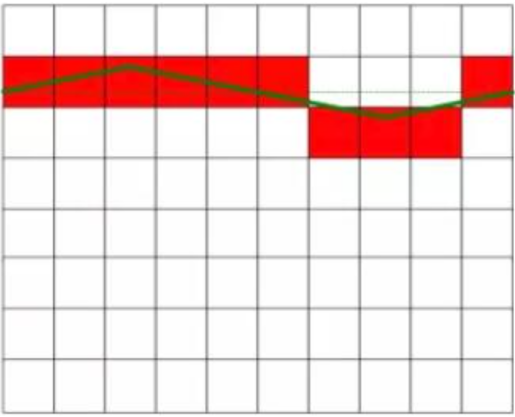
ໃຊ້ແຮງດັນໄຟຟ້າ DC ລົບກວນທີ່ມີຄ່າສະເລ່ຍເປັນສູນ
ໃນສອງກໍລະນີໃນຮູບຂ້າງເທິງນີ້, ໃຫ້ວັດແທກກະແສໄຟຟ້າໂດຍກົງ 10 ຄັ້ງ, ແລະ ຈາກນັ້ນໃຫ້ເອົາຄ່າສະເລ່ຍຂອງການວັດແທກ 10 ຄັ້ງ.
ຂະໜາດທຳອິດທາງຊ້າຍຖືກວັດແທກ 10 ເທື່ອ, ແລະການອ່ານແມ່ນຄືກັນໃນແຕ່ລະຄັ້ງ. ເນື່ອງຈາກອິດທິພົນຂອງຄວາມຜິດພາດໃນການວັດແທກ AD, ການອ່ານແຕ່ລະຄັ້ງແມ່ນ 7V. ຫຼັງຈາກການວັດແທກໂດຍສະເລ່ຍ 10 ຄັ້ງ, ຜົນໄດ້ຮັບຍັງຄົງເປັນ 7V. ຄວາມຜິດພາດໃນການວັດແທກ AD ແມ່ນ 0.7V, ແລະຄວາມຜິດພາດໃນການວັດແທກແມ່ນ 0.7V.
ຂະໜາດທີສອງຢູ່ເບື້ອງຂວາໄດ້ມີການປ່ຽນແປງຢ່າງຫຼວງຫຼາຍ:
ເນື່ອງຈາກຄວາມແຕກຕ່າງໃນດ້ານບວກ ແລະ ດ້ານລົບຂອງແຮງດັນແຊກແຊງ ແລະ ຄວາມກວ້າງຂອງຄື້ນ, ຄວາມຜິດພາດໃນການວັດແທກ AD ແມ່ນແຕກຕ່າງກັນຢູ່ຈຸດວັດແທກທີ່ແຕກຕ່າງກັນ. ພາຍໃຕ້ການປ່ຽນແປງຂອງຄວາມຜິດພາດໃນການວັດແທກ AD, ຜົນການວັດແທກ AD ຈະປ່ຽນແປງລະຫວ່າງ 6V ແລະ 7V. ເຈັດໃນການວັດແທກແມ່ນ 7V, ມີພຽງສາມຢ່າງເທົ່ານັ້ນທີ່ເປັນ 6V, ແລະ ຄ່າສະເລ່ຍຂອງ 10 ການວັດແທກແມ່ນ 6.3V! ຄວາມຜິດພາດແມ່ນ 0V!
ໃນຄວາມເປັນຈິງ, ບໍ່ມີຄວາມຜິດພາດໃດເປັນໄປບໍ່ໄດ້, ເພາະວ່າໃນໂລກວັດຖຸປະສົງ, ບໍ່ມີ 6.3V ທີ່ເຂັ້ມງວດ! ຢ່າງໃດກໍຕາມ, ມີແທ້ໆ:
ໃນກໍລະນີທີ່ບໍ່ມີການແຊກແຊງ, ເນື່ອງຈາກຜົນການວັດແທກແຕ່ລະຄັ້ງແມ່ນຄືກັນ, ຫຼັງຈາກວັດແທກສະເລ່ຍ 10 ຄັ້ງ, ຄວາມຜິດພາດຍັງຄົງບໍ່ປ່ຽນແປງ!
ເມື່ອມີການແຊກແຊງໃນປະລິມານທີ່ເໝາະສົມ, ຫຼັງຈາກການວັດແທກ 10 ຄັ້ງຖືກສະເລ່ຍ, ຄວາມຜິດພາດໃນການວັດແທກ AD ຈະຫຼຸດລົງຕາມລຳດັບຄວາມກວ້າງ! ຄວາມລະອຽດໄດ້ຮັບການປັບປຸງຕາມລຳດັບຄວາມກວ້າງ! ຄວາມຖືກຕ້ອງຂອງການວັດແທກຍັງໄດ້ຮັບການປັບປຸງຕາມລຳດັບຄວາມກວ້າງ!
ຄຳຖາມຫຼັກແມ່ນ:
ມັນຄືກັນບໍເມື່ອແຮງດັນທີ່ວັດແທກໄດ້ແມ່ນຄ່າອື່ນໆ?
ຜູ້ອ່ານອາດຈະຕ້ອງການປະຕິບັດຕາມຂໍ້ຕົກລົງກ່ຽວກັບການແຊກແຊງໃນພາກທີສອງ, ສະແດງຄວາມແຊກແຊງດ້ວຍຊຸດຂອງຄ່າຕົວເລກ, ວາງການແຊກແຊງຊ້ອນກັນໃສ່ແຮງດັນທີ່ວັດແທກໄດ້, ແລະຈາກນັ້ນຄິດໄລ່ຜົນການວັດແທກຂອງແຕ່ລະຈຸດຕາມຫຼັກການການນຳຂອງຕົວແປງ AD, ແລະຈາກນັ້ນຄິດໄລ່ຄ່າສະເລ່ຍສຳລັບການກວດສອບ, ຕາບໃດທີ່ຄວາມກວ້າງຂອງການແຊກແຊງສາມາດເຮັດໃຫ້ການອ່ານຫຼັງຈາກການວັດປະລິມານ AD ປ່ຽນແປງ, ແລະຄວາມຖີ່ຂອງການເກັບຕົວຢ່າງສູງພຽງພໍ (ການປ່ຽນແປງຄວາມກວ້າງຂອງການແຊກແຊງມີຂະບວນການປ່ຽນແປງ, ແທນທີ່ຈະເປັນສອງຄ່າທີ່ເປັນບວກ ແລະ ລົບ), ແລະຄວາມຖືກຕ້ອງຕ້ອງໄດ້ຮັບການປັບປຸງ!
ສາມາດພິສູດໄດ້ວ່າຕາບໃດທີ່ແຮງດັນທີ່ວັດແທກໄດ້ບໍ່ແມ່ນຈຳນວນເຕັມ (ມັນບໍ່ມີຢູ່ໃນໂລກວັດຖຸປະສົງ), ຈະມີຄວາມຜິດພາດໃນການວັດແທກ AD, ບໍ່ວ່າຄວາມຜິດພາດໃນການວັດແທກ AD ຈະໃຫຍ່ປານໃດ, ຕາບໃດທີ່ຄວາມກວ້າງຂອງການແຊກແຊງສູງກວ່າຄວາມຜິດພາດໃນການວັດແທກ AD ຫຼືສູງກວ່າຄວາມລະອຽດຕໍ່າສຸດຂອງ AD, ມັນຈະເຮັດໃຫ້ຜົນການວັດແທກປ່ຽນແປງລະຫວ່າງສອງຄ່າທີ່ຢູ່ຕິດກັນ. ເນື່ອງຈາກການແຊກແຊງມີຄວາມສົມມາດທາງບວກ ແລະ ທາງລົບ, ຂະໜາດ ແລະ ຄວາມເປັນໄປໄດ້ຂອງການຫຼຸດລົງ ແລະ ການເພີ່ມຂຶ້ນຂອງແມ່ນເທົ່າກັນ. ດັ່ງນັ້ນ, ເມື່ອຄ່າຕົວຈິງໃກ້ຄຽງກັບຄ່າໃດ, ຄວາມເປັນໄປໄດ້ຂອງຄ່າທີ່ຈະປາກົດແມ່ນສູງກວ່າ, ແລະ ມັນຈະໃກ້ຄຽງກັບຄ່າໃດຫຼັງຈາກການຫາຄ່າສະເລ່ຍ.
ນັ້ນຄື: ຄ່າສະເລ່ຍຂອງການວັດແທກຫຼາຍຄັ້ງ (ຄ່າສະເລ່ຍຂອງການແຊກແຊງແມ່ນສູນ) ຕ້ອງໃກ້ກັບຜົນການວັດແທກໂດຍບໍ່ມີການແຊກແຊງ, ນັ້ນຄື, ການໃຊ້ສັນຍານແຊກແຊງ AC ທີ່ມີຄ່າສະເລ່ຍເປັນສູນ ແລະ ການຫາຄ່າສະເລ່ຍຂອງການວັດແທກຫຼາຍຄັ້ງສາມາດຫຼຸດຜ່ອນຄວາມຜິດພາດໃນການວັດແທກ AD ທີ່ທຽບເທົ່າ, ປັບປຸງຄວາມລະອຽດຂອງການວັດແທກ AD, ແລະ ປັບປຸງຄວາມຖືກຕ້ອງຂອງການວັດແທກ!
ເວລາໂພສ: ວັນທີ 13 ກໍລະກົດ 2023




